@TOC
合并两个有序链表
这道题,很容易就想到解决办法了,两个链表相互比较,较小的进入链表。需要注意的是临时节点需要新分配空间,否则每次都会把临时节点都会删除掉详细介绍可见,导致答案错误。
AC代码为:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
ListNode *res;
if(l1 == NULL) return l2;
if(l2 == NULL) return l1;
if(l1->val < l2->val) {
res = l1;
}else {
res = l2;
l2 = l1;
}
ListNode *head = res;
ListNode *pre = res;
while(l2 != NULL) {
if(res == NULL) {
pre->next = l2;
break;
}
if(res->val > l2->val) {
ListNode *tmp = new ListNode(l2->val);
tmp->next = pre->next;
pre->next = tmp;
pre = tmp;
l2 = l2->next;
}else {
pre =res;
res = res->next;
}
}
return head;
}
};
括号生成
这道题的解题方案分为两步走,首先需要生成n个左括号和n个右括号排列而成的字符串,然后对这些字符串进行筛选符合要求的存到容器中。
我认为这道题的难点在于如何全排列,因为筛选很简单,只需要遍历字符串保证左括号数目是一直大于等于右括号数目即可。
全排列有两种方式,一是利用泛型算法next_permutation()函数,二是手撸递归。
AC代码为:
利用next_permutation
class Solution {
public:
vector<string> generateParenthesis(int n) {
vector<string> res;
string ori(n, '(');
ori = ori.append(n, ')');
res.push_back(ori);
while (next_permutation(ori.begin(), ori.end())) {
int sum = 0;
for(auto scan = ori.begin(); scan != ori.end(); ++scan) {
if(*scan == '(') sum++;
else sum--;
if(sum < 0) break;
}
if(sum == 0) res.push_back(ori);
}
return res;
}
};
手撸递归
class Solution {
public:
vector<string> generateParenthesis(int n) {
vector<string> res;
func(res, "", 0, 0, n);
return res;
}
void func(vector<string> &res, string str, int l, int r, int n){
if(l > n || r > n || r > l) return ;
if(l == n && r == n) {res.push_back(str); return;}
func(res, str + '(', l+1, r, n);
func(res, str + ')', l, r+1, n);
return;
}
};
合并K个排序链表
做这道题本来的想法是利用之前的合并两个排序链表为基础,循环链表容器达到目的。但是实施的时候又考虑到越到后面目的链表越来越长,会有很多重复的对比操作。最后写的时候不自觉的暴力ac了,哎,可悲
AC代码:
class Solution {
public:
ListNode* mergeKLists(vector<ListNode*>& lists) {
ListNode *res = new ListNode(0);
ListNode *head = res;
vector<ListNode *> scan;
vector<int> tmp;
for(auto start = lists.begin(); start != lists.end(); ++start) {
ListNode *ope = *start;
while(ope != NULL) {
tmp.push_back(ope->val);
ope = ope->next;
}
}
sort(tmp.begin(), tmp.end());
for(auto i : tmp) {
ListNode *ope = new ListNode(i);
res->next = ope;
res = ope;
}
return head->next;
}
};
两两交换链表中的节点
难点是如何交换两个节点,题目说明不是交换两个值,而是交换两个节点。
交换过程如下:
初始情况,需要交换first和second节点:
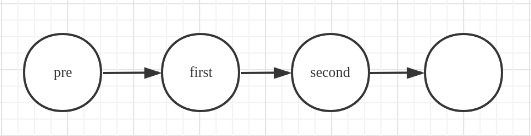
交换操作
pre->next = second;
first->next = second->next;
second->next = first;
交换后:
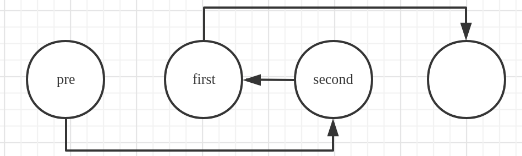
AC代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* swapPairs(ListNode* head) {
ListNode *first = head;
ListNode *pre = new ListNode(0);
pre->next = first;
ListNode *res = pre;
while(first != NULL && first->next != NULL) {
ListNode *second = first->next;
//swap
pre->next = second;
first->next = second->next;
second->next = first;
//default
pre = first;
first = first->next;
}
return res->next;
}
};
K 个一组翻转链表
照常的先定义一个头前指针记录返回头结点。
解决方案为,k个一组依次翻转链表。
本来想用递归翻转,奈何递归憋不出来,遂放弃,标记一下自己
AC代码为:
class Solution {
public:
ListNode* reverseKGroup(ListNode* head, int k) {
if(k == 1) return head;
ListNode *res = new ListNode(0);
res->next = head;
ListNode *pre = res;
ListNode *first = pre->next;
int sc = k;
while(pre->next != NULL) {
ListNode *lpre = pre;
ListNode *scan = pre;
int l = sc;
while(l != 0) {
lpre = scan;
scan = scan->next;
if(scan == NULL) return res->next;
l--;
}
if(scan == first) {
pre = first;
first = pre->next;
sc = k;
}else {
lpre->next = scan->next;
pre->next = scan;
scan->next = first;
pre = scan;
sc--;
}
}
return res->next;
}
};
翻转的递归函数:
递归的思想就是从递归的终点往回推
大概的过程可以表现为(假设k=4):
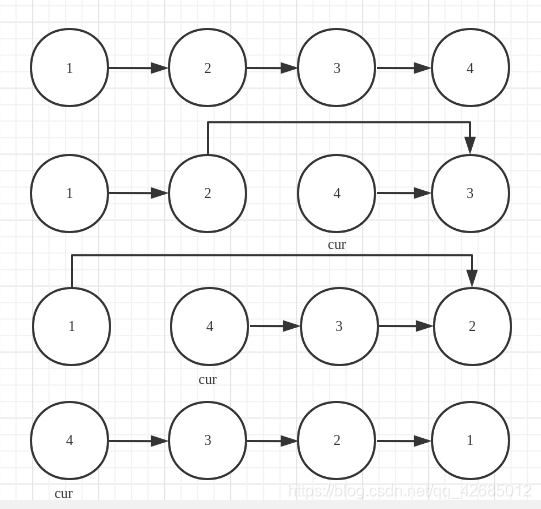
ListNode* reverse(ListNode* head,int k){
if(k==1)return head;
ListNode*cur=reverse(head->next,k-1);
head->next->next=head;
head->next=NULL;
return cur;
}
删除排序数组中的重复项
这道题确实如标签”简单”一样,在解题中想到的就是一个迭代器定位,另外一个迭代器扫描,删除相同的数字。这样操作是能够AC的,但是一直没有明白题目中的 “原地”修改输入数组 到底代表什么,看官方解题后理解了,原来是这么个原地的意思: 原地的意思值,我们可以通过两个指针直接修改,不需要删除元素,直接修改成不重复的元素就可以了,而且题目也已经表示不需要考虑数组中超出新长度后面的元素。西八~~ 提示有够多的
AC代码:
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if(nums.size() < 2) return nums.size();
auto start = nums.begin();
auto scan = start + 1;
while(scan != nums.end()) {
if(*scan != *start) {
start = scan;
scan = start + 1;
}else {
//使用迭代器erase会使原迭代器失效,但是会返回原迭代器的下一个迭代器
scan = nums.erase(scan);
}
}
return nums.size();
}
};
官方给出的代码:
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if (nums.size() == 0) return 0;
int i = 0;
for (int j = i + 1; j < nums.size(); j++) {
if (nums[j] != nums[i]) {
i++;
nums[i] = nums[j];
}
}
return i + 1;
}
};
移除元素
这道题和上面的题目很相似,但是我深受PrimerC++影响,使用迭代器遍历一遍也可以达到目的。和上一题类似。
AC代码:
class Solution {
public:
int removeElement(vector<int>& nums, int val) {
int len = nums.size();
for(auto scan = nums.begin(); scan < nums.end();) {
if(*scan == val) {
scan = nums.erase(scan);
len--;
}else {
++scan;
}
}
return len;
}
};
实现 strStr()
解这道题的思路就是,遍历haystack,寻找和needle第一个字符相同的字符,然后双指针同时遍历两个字符串,若能把needle遍历完,则返回位置。否则继续遍历haystack。
然后发现超时了,遂想到遍历haystack的时候可以提前终止循环,即当遍历时haystack剩余的长度小于needle长度的时候,直接退出循环即可。:) 又是双百
ps: 当needle为空字符串的时候,应当返回0。
AC代码
class Solution {
public:
int strStr(string haystack, string needle) {
int res = -1;
if(needle.size() == 0 ) return 0;
for(int i = 0; i < haystack.size(); ++i) {
if(haystack.size() - i < needle.size()) break;
int j = 0;
if(haystack[i] == needle[j]) {
for(int k = i; j < needle.size(); ++j, ++k) {
if(haystack[k] != needle[j]) break;
}
}
if(j == needle.size()) return i;
else res = -1;
}
return res;
}
};
在看完官方给的解题答案的时候,秒啊,利用哈希码来完成字符和位置的绑定,最后通过对比哈希值即可实现搜索的目的。属实nb
具体操作可以简化为:
1 char类型 a, b, c, d, .., z 对应 int类型 0, 1, 2, 3, …, 25
2 然后位置通过26进制实现
eg.
ab = 0*26^1^+1*26^0^
不过在具体代码实现中,需要考虑溢出的情况
两数相除
看到这道题,脑海中浮现辗转相除法以及十进制转二进制的算法,这不就是循环用被除数减去除数就可以达到目的吗?心中不免疑惑这就是中等题吗
果然,too young too simple 暴力总有超时等候
然后想既然不能如此暴力,那么可不可以通过模拟乘法或者模拟除法呢,利用数组就可以办到。
利用一个vector记录divisor的倍数,另外一个vector记录相应倍数需要加的值
AC代码为:
class Solution {
public:
int divide(int dividend, int divisor) {
if(divisor == 1) return dividend;
if(divisor == -1) {
if(dividend != INT_MIN) return dividend * -1;
else return INT_MAX;
}
int res = 0;
int sign = -1;
int sign_1 = -1;
//避免出现INT_MIN,在后面的操作默认全为负数
if(dividend > 0) {
dividend *= -1;
sign = 1;
}
if(divisor > 0) {
divisor *= -1;
sign_1 = 1;
}
//既然不能乘法除法运算,用vector记录divisor的倍数,以及相应倍数需要加的结果
int mid = divisor;
vector<int> div;
div.push_back(mid);
int midres = 1;
vector<int> vres;
vres.push_back(midres);
while(mid > INT_MIN / 2) {
mid += mid;
if(mid < dividend) break;
div.push_back(mid);
midres += midres;
vres.push_back(midres);
}
auto dend = div.rbegin();
auto vend = vres.rbegin();
for(dend; dend != div.rend(); ++dend, ++vend) {
//利用divisor的倍数,dividend每次减去能减的最大倍数
if(dividend <= *dend) {
dividend -= *dend;
res += *vend;
}
}
while(dividend <= divisor) {
dividend -= divisor;
res++;
}
return res*sign*sign_1;
}
};
串联所有单词的子串
通过利用map将words的字符串和其需要匹配的次数存下来,然后遍历字符串s,每次取需要匹配的字符的长度,通过map判断是否存在,如果存在的话,创建一个map副本,然后循环看最后是否能将这个map副本全部清除,是的话则表明能够全部匹配,否则继续遍历字符串s,直到s剩余的长度小于words容器全部字符串的长度。
AC代码:
class Solution {
public:
vector<int> findSubstring(string s, vector<string>& words) {
vector<int> res;
if((s.size() == 0) || (words.size() == 0) || (s.size() < words.size())) return res;
map<string, int> wo;
for(auto scan = words.begin(); scan != words.end(); ++scan) {
if(wo.find(*scan) == wo.end()) {
wo[*scan] = 1;
}else {
wo[*scan] ++;
}
}
int len = (*words.begin()).size();
for(int i = 0; s.size() - i >= words.size() * len; ++i) {
string tmp = s.substr(i, len);
if(wo.find(tmp) != wo.end()) {
//cout << "zl " << tmp << endl;
int j = i;
map<string, int> ope(wo.begin(), wo.end());
while(ope.find(tmp) != ope.end()) {
ope[tmp]--;
if(ope[tmp] == 0) ope.erase(tmp);
j += len;
tmp = s.substr(j, len);
//cout << "zll " << tmp << endl;
}
//cout << "zlll " << ope.size() << endl;
if(ope.size() == 0) res.push_back(i);
}
}
return res;
}
};





