@TOC
下一个排列
看到这道题,下意识的想到之前遇到的next_permutation()函数;不过这样的话这道题就失去了意义。
一番思考,解决这道题需要倒序思考。思考历程如下:
需要找下一个排列,关键是需要找到最后一个挨着的顺序组合,例如12345中45。
考虑到需要找最后一个,何不从最后开始遍历,找到第一个倒序挨着的组合。
当我们找到之后,还需要考虑是不是直接交换这两个数字
如果直接交换的话,像之前的例子12345,则会变成12354。成功
但是例如1235432,则会变成1253432。离谱(正确为1242335)
问题出现了,当从后往前找到第一个倒序挨着的组合35之后,还需要考虑5之后的数字(是一个递减的数组)是否存在大于5前面这个3,如果存在的话,找到最后一个大于3的(例子中的4),然后和3交换,之后将这个交换的数组递增排序。
AC代码:
class Solution {
public:
void nextPermutation(vector<int>& nums) {
int n = nums.size();
bool flag = 1;
for(auto scan = nums.rbegin(); scan != nums.rend() - 1; ++scan) {
if(*(scan) > *(scan + 1)) {
auto swap = scan;
while(swap > nums.rbegin()) {
swap--;
if(*swap <= *(scan+1)) {
swap++;
break;
}
if(swap == nums.rbegin()) break;
}
iter_swap((scan + 1), swap);
sort(nums.rbegin(), scan + 1, [](int a, int b){return a>b;});
return;
}
}
if(flag) sort(nums.begin(), nums.end());
}
};
最长有效括号
看到这道题目,心中最开始联想到的是之前做的一道题,用来滑动窗口来记录最长字符串,用栈来判断括号的有效性,然后发现,总是缺点什么,边界情况考虑的不到位。后面尝试暴力解决,发现超时,而且总是觉得暴力不优美。又尝试遍历字符串记录左右括号的个数,但是还是没有解决。就这样,思路满天开花,但是一个都不能AC,后面忍不住看了解题,发现还可以用动态规划来做,在解题的时候没有想到,所以就用了动态规划来解题。
具体的思路为
初始化数组为0.
从左往右遍历,遇到左括号跳过,遇到右括号判断,有两种情况:
- 右括号左边是左括号,那么
dp[i] = dp[i-2] + 2; - 右括号左边还是右括号,那么
dp[i] = dp[i-1] + dp[i - dp[i-1] -2] + 2
理想状态时如下:

当然上面考虑的都是成功匹配的情况下,需要考虑的特殊情况为:
- i - 2 < 0
- dp[i-1] = 0
- i - dp[i-1] - 2 < 0
- s[i - dp[i-1] -1] = ‘)’
AC代码:
class Solution {
public:
int longestValidParentheses(string s) {
int res = 0;
int dp[s.size()];
memset(dp, 0, sizeof(dp));
for (int i = 1; i < s.length(); i++) {
if(s[i] == ')') {
if(s[i-1] == '(') dp[i] = i > 2 ? dp[i-2] + 2 : 2;
if(s[i-1] == ')' && dp[i-1] != 0 && i - dp[i-1] - 1 >= 0 && s[i - dp[i-1] - 1] == '(') {
dp[i] = dp[i-1] + 2 + ( i - dp[i-1] - 2 >= 0 ? dp[i - dp[i-1] - 2] : 0 );
}
res = res > dp[i] ? res : dp[i];
}
}
return res;
}
};
搜索旋转排序数组
这道题的算法时间复杂度要求必须是 O(log n) 级别。
这就是明确必须要使用二分查找完成。
思路有两个,第一种是首先二分查找找到旋转的地方,然后根据target值确定是用二分查找旋转左边的还是旋转右边的。
第二种是每次查找的时候,根据中位值判断有序的数组是前半部分还是后半部分。因为旋转后的数组特点就是后面的部分总是小于前面的部分。所以就可以看中位值是否大于等于左边的值,如果是,则表明该中位值是在左边的部分,然后再根据target的值判断它是在前半部分还是后半部分。
AC代码:
class Solution {
public:
int search(vector<int>& nums, int target) {
int l = 0;
int r = nums.size()-1;
if((nums.size() == 0) || (target < nums[l] && target > nums[r])) return -1;
while(l <= r) {
int mid = l + (r - l) / 2;
if(nums[mid] == target) return mid;
if (nums[l] <= nums[mid]) {
if (target >= nums[l] && target < nums[mid]) {
r = mid - 1;
} else {
l = mid + 1;
}
} else {
if (target <= nums[r] && target > nums[mid]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
};
在排序数组中查找元素的第一个和最后一个位置
这道题算是对二分法的一个扩展,即寻找数组中元素的左右边界。而且题目时间复杂度已经明确使用二分法,所以解题方法也就是在二分法的基础上修改,如何找到左右边界呢?可以在二分法查找的基础上,在找到值之后,在这个地方修改,再找到值之后不是返回值的位置,而是继续缩小范围查找,即可满足左右边界的要求。其实就是找到第一个小于等于这个值的下标,以及第一个大于这个值的下标。
AC代码如下:
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
int l = -1, r = -1;
int left = 0, right = nums.size();
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) left = mid + 1;
else if(nums[mid] < target) left = mid + 1;
else right = mid;
}
r = left;
left = 0, right = nums.size();
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) right = mid;
else if(nums[mid] < target) left = mid + 1;
else right = mid;
}
l = left;
if(l == r) return {-1, -1};
return {l, r-1};
}
};
搜索插入位置
继续二分查找,这道题应该是二分查找最简单的题目了,为什么还在前面两道题的后面呢~
是官方告诉我们先苦后甜吗?
AC代码:
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0, right = nums.size();
while(left < right) {
int mid = left + (right - left) / 2;
if(nums[mid] == target) return mid;
else if(nums[mid] < target) left = mid + 1;
else right = mid;
}
return left;
}
};
有效的数独
玩过数独的人都应该知道,一个有效的9*9数独必须要满足每行每列每3*3宫1-9数字都不重复。
看到题目给的三个要求,第一反应就是每行每列没3*3依次判断是否符合要求,但是作为中等题目,还是应该有优化的方式的,可以想象一下,每行每列每3*3宫格必须要循环三次吗?循环一次然后依次判断行,列,宫格是否重复也可以达到要求呢?
行和列是比较好判断两层循环的时候,会有i和j指明是哪行哪列,如何判断当前是字符是属于哪个宫格就比较棘手。
假设我们将宫格像下面分类,可以看到我们可以通过行和列来确定宫格数:(i/3)*3 + j/3
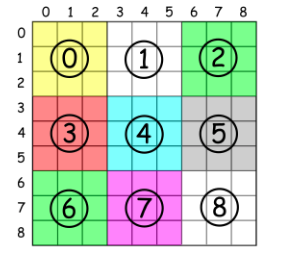
ps:刚开始用map<int, set<char>>来记录,发现不仅时间长,空间还用的多。map,set虽好用但是占空间耗时间相对于数组。
AC代码:
class Solution {
public:
bool isValidSudoku(vector<vector<char>>& board) {
int row[9][9];
int column[9][9];
int base_box[9][9];
memset(row, 0, sizeof(row));
memset(column, 0, sizeof(column));
memset(base_box, 0, sizeof(base_box));
for(int i = 0; i < 9; ++i) {
for(int j = 0; j < 9; ++j) {
if(board[i][j] == '.')continue;
else {
int num = board[i][j] - '0' -1;
if(row[i][num] == 0) row[i][num] = 1;
else return false;
if(column[j][num] == 0) column[j][num] = 1;
else return false;
if(base_box[(i/3)*3 + (j/3)][num] == 0) base_box[(i/3)*3 + (j/3)][num] = 1;
else return false;
}
}
}
return true;
}
};
解数独
和平常自己解数独的方式不同,我平常解数独的方式一般都是根据行列宫格的限制寻找一个正确的位置放置正确的数字,然后根据这个数字再次扩大限制条件,这样一步步的解答。但是有的时候没有突破点的时候,会假设,然后推导。
但是计算机可能不太好实现这种思维,但是它有着强大的计算能力,也就是说,它能够使用假设推导的方式一遍遍的去尝试,直到完成整个数组。但是如果毫无约束的填写会导致大量的时间浪费。在推导的时候,需要加上行列宫格的限制,这样能优化很多。
AC代码:
class Solution {
public:
int row[9][9] = {0};
int column[9][9] = {0};
int base_box[9][9] = {0};
bool finished = false;
void setNum(int r, int c, int num, vector<vector<char>>& board) {
row[r][num] = 1;
column[c][num] = 1;
base_box[(r/3)*3+(c/3)][num] = 1;
board[r][c] = num + 1 + '0';
}
void removeNum(int r, int c, int num, vector<vector<char>>& board) {
row[r][num] = 0;
column[c][num] = 0;
base_box[(r/3)*3+(c/3)][num] = 0;
board[r][c] = '.';
}
bool back(int r, int c, vector<vector<char>>& board) {
if(r == 9) {
finished = true;
return true;
}
if(board[r][c] == '.') {
for(int i = 0; i < 9; i++) {
if(row[r][i] == 0 && column[c][i] == 0 && base_box[(r/3)*3+(c/3)][i] == 0) {
setNum(r, c, i, board);
if(c == 8) back(r+1, 0, board);
else back(r, c+1, board);
if(!finished) {
removeNum(r, c, i, board);
}
}
}
}else {
if(c == 8) back(r+1, 0, board);
else back(r, c+1, board);
}
return false;
}
void solveSudoku(vector<vector<char>>& board) {
//init
for(int i = 0; i < 9; ++i) {
for(int j = 0; j < 9; ++j) {
if(board[i][j] == '.') continue;
else {
int num = board[i][j] - '0' - 1;
setNum(i, j, num, board);
}
}
}
//back
back(0, 0, board);
}
};
外观数列
这道题题目有点拗口,比较晦涩难懂,描述为下:

主要难以理解的点在于序列的每一项都是对前一项的描述。其实可以忽略每一项前面的1. 2. 3. 4. 5.这样可能就好理解了, 11 是对 1 的描述, 21 是对 11 的描述, 1211是对 21 的描述,这样依次类推。
看到n属于[1,30],暴力跃跃欲试。但是还是极力止住了这个想法,用递归加缓存数组解决。
AC代码:
class Solution {
public:
map<int, string> res;
string results(int n) {
string s;
int count = 0;
char pre = res[n][0];
for(auto scan = res[n].begin(); scan != res[n].end(); ++scan) {
if(*scan == pre) {
count++;
}else {
s.append(to_string(count) + pre);
count = 1;
pre = *scan;
}
}
s.append(to_string(count) + pre);
res[n+1] = s;
return res[n+1];
}
string countAndSay(int n) {
if(n == 1) {
res[1] = "1";
return res[1];
}
if(res.find(n) == res.end()) {
res[n] = countAndSay(n - 1);
return results(n-1);
}else {
return results(n-1);
}
}
};
组合总和
这道题,容易想到的解决办法就是先排序之后,遍历数组从最小的数累加到最大的小于目标数字为止然后再次遍历数组寻找解。例如[2,3,5,7],target = 7,首先把path容器变成[2,2,2],遍历数组找到合适的,然后容器变成[2,2],再次遍历数组,这样依次类推。由于第一层遍历的关系,后面的数字不会用到前面的数字可以排除重复解。
ps:coding能力是在太鸡肋了,希望早日能够练就把思想转化为代码的能力。
AC代码:
class Solution {
public:
vector<int> ori;
vector<vector<int>> res;
vector<int> path;
void findRes(int start, int target) {
if (target == 0) {
res.push_back(path);
return;
}
for (int i = start; i < ori.size() && target - ori[i] >= 0; i++) {
path.push_back(ori[i]);
findRes(i, target - ori[i]);
path.pop_back();
}
}
vector<vector<int>> combinationSum(vector<int> &candidates, int target) {
sort(candidates.begin(), candidates.end());
ori = candidates;
findRes(0, target);
return res;
}
};
组合总和 II
相对于上一题,要求改变的地方有两点,一是不允许重复使用某个数字,二是给定的数组中允许出现重复的数字;
因为重复数字的出现,导致结果可能会有重复,所以在找到结果后判断是否存在去除重复解。
AC代码:
class Solution {
public:
vector<int> ori;
vector<vector<int>> res;
vector<int> path;
void findRes(vector<int>::iterator iter, int target) {
if(target == 0) {
if(find(res.begin(), res.end(), path) == res.end()) res.push_back(path);
return;
}
for(auto scan = iter; scan != ori.end() && target - *scan >= 0; scan++) {
path.push_back(*scan);
findRes(scan + 1, target - *scan);
path.pop_back();
}
}
vector<vector<int>> combinationSum2(vector<int> &candidates, int target) {
sort(candidates.begin(), candidates.end());
ori = candidates;
findRes(ori.begin(), target);
return res;
}
};
ps:看了一下题解,发现在for循环里面加上 if(scan > iter && *scan == *(scan - 1)) continue;能够去除重复解,可以避免每次查找花费的时间。





