@TOC
缺失的第一个正数

思路,一开始想到的是排序后二分查找到第一个大于0的地方,然后从1开始查找第一个缺失的正数。不过这个一用排序时间复杂度就不达标了,后面也是看了题解,可以用哈希表的思想原地的修改其对应关系。

AC代码:
class Solution {
public:
int firstMissingPositive(vector<int>& nums) {
if(nums.size() == 0 ) return 1;
int n = nums.size();
for(int i = 0; i < n; ++i) {
if(nums[i] <= 0 || nums[i] > n) nums[i] = n + 1;
}
for(int i = 0; i < n; ++i) {
int a = abs(nums[i]);
if(a < n + 1) nums[a-1] = -abs(nums[a-1]);
}
for(int i = 0; i < n; ++i) {
if(nums[i] > 0) return i + 1;
}
return n + 1;
}
};
接雨水

这道题和之前遇到过的”盛最多水的容器”题目看起来好像是差不多的,所以下意识的就会选择用双指针来解题。
解题的关键,如何计算每个点接的多少水;
之前在考虑的时候出现一种错觉,就是在计算能接受多少水考虑的是大范围的计算,没有想到可以通过该点的情况直接计算某一点能存储的水量。只有当把这道题想到可以分解成一个一个去计算的时候,双指针法才会更加的明了。
双指针扫描还是和之前一样,移动较小的那一边,这样能够保证另外一边最高值总是大于小的那一边的,不过在移动过程中,记录左边和右边的最高值。而在扫描的时候,就能判断出某点能存储的水量是等于属于哪边的最高值-该点的数值。扫描结束即可得到答案。
AC代码:
class Solution {
public:
int trap(vector<int>& height) {
int sum = 0;
if(height.size() <= 2) return sum;
int left = 0, right = height.size() -1;
int l_max = 0, r_max = 0;
while(left < right) {
if(height[left] < height[right]) {
l_max = max(l_max, height[left]);
sum += l_max - height[left];
left++;
}else {
r_max = max(r_max, height[right]);
sum += r_max - height[right];
right--;
}
}
return sum;
}
};
字符串相乘

解题思路就是,刚学习乘法的时候用到的办法,也就是大数相乘在草稿纸打草稿的过程。先拆分一个字符串,用该字符串的每一个字符去乘另一个字符串,然后累加结果。需要注意的是处理进位,乘法和加法都需要考虑进位。
AC代码:
class Solution {
public:
vector<string> vs;
//相乘计算,loc表示p是第几位,个位为0,十位为1,以此类推
void mul(string& num, char p, int loc) {
int i = p - '0';
//进位
int sign = 0;
string res;
//模拟乘法
for(auto fir = num.rbegin(); fir != num.rend(); ++fir) {
int j = *fir - '0';
int m = i * j + sign;
sign = m / 10;
char r = m % 10 + '0';
res = r + res;
}
if(sign != 0){
char s = sign + '0';
res = s + res;
}
//需要处理每个位置相乘的情况
res = res.append(loc, '0');
vs.push_back(res);
}
//将每个位置相乘的结果累加
string add() {
if(vs.size() == 1) return *vs.begin();
string res = *vs.begin();
//模拟加法
for(auto fir = vs.begin() + 1; fir != vs.end(); ++fir) {
int lenf = (*fir).size() - 1;
int lenr = res.size() - 1;
string needadd(lenf-lenr, '0');
res = needadd + res;
int sign = 0;
string restmp;
while(lenf != -1) {
int r = res[lenf] - '0';
int f = (*fir)[lenf] - '0';
int sum = r + f + sign;
sign = sum / 10;
char remain = sum%10 + '0';
restmp = remain + restmp;
lenf--;
}
if(sign != 0){
char s = sign + '0';
restmp = s + restmp;
}
res = restmp;
}
return res;
}
string multiply(string num1, string num2) {
//保证num1是序列较长的数列
if(num1.size() < num2.size()) {
string tmp = num2;
num2 = num1;
num1 = tmp;
}
if(num1 == "0" || num2 == "0") return "0";
int i = 0;
for(auto fir = num2.rbegin(); fir != num2.rend(); ++fir, ++i) {
mul(num1, *fir, i);
}
return add();
}
};
看了题解之后,好像下面这种方法更能优化性能,真厉害

通配符匹配

这道题着实把我恶心到了

因为之前遇到过正则匹配的问题,很容易的想到递归解决问题,但是没有想到的是,超时伴随我一个下午,期间经历怀疑自我,想换个方法等等一系列的思考。到最后还被数组又给恶心一遍。说到底,只恨自己不够强大,,,
解题思路很简单,递归
/**
*ls记录s匹配的位置,lp记录p匹配的位置
*ls == s.size() && lp == p.size(),表明全部匹配,返回true;
*ls == s.size() && p.substr(lp, p.size()) == string(p.size()-lp, '*'),表面p剩余的字符串全部为*,返回true;否则返回false
*lp == p.size() && ls != s.size(),表面p已经匹配完,但是s还没完,返回false
*递归的情况有下面两种
*1: (s[ls]==p[lp] || p[lp] == '?') 则递归(s, p, ls+1, lp+1)
*2: p[lp] == '*' 则递归(s, p, ls+1, lp) 和 (s, p, ls,lp+1)
*否则说明匹配失败,返回false
*处理超时的两种措施
*1: 把*...*变成*; 2: 添加备忘缓存避免重复递归
*/
AC代码:
class Solution {
public:
//这个数组大小还让我头疼了一会儿,小了例子过不去,大了超时,吐了
int remem[1100][1100];
int resMatch(string& s, string& p, int ls, int lp) {
//cout << ls <<" "<< lp <<" "<< remem[ls][lp] << endl;
if(remem[ls][lp] != -1) return remem[ls][lp];
if(lp == p.size() && ls == s.size()) return remem[ls][lp] = 1;
if(lp == p.size() && ls != s.size()) return remem[ls][lp] = 0;
if(ls == s.size() && lp != p.size()) {
string remain = p.substr(lp, p.size());
string suc(p.size()-lp, '*');
if(remain == suc) return remem[ls][lp] = 1;
else return remem[ls][lp] = 0;
}
if(s[ls] == p[lp] || p[lp] == '?') {
return remem[ls][lp] = resMatch(s, p, ls+1, lp+1);
}
else if(p[lp] == '*') {
if(lp != 0 && p[lp-1] == '*') return remem[ls][lp] = resMatch(s, p, ls, lp+1);
return remem[ls][lp] = (resMatch(s, p, ls, lp+1) || resMatch(s, p, ls+1, lp));
}else {
return remem[ls][lp] = 0;
}
}
bool isMatch(string s, string p) {
memset(remem, -1, sizeof(remem));
//cout << s.size() << p.size() << endl;
return resMatch(s, p, 0, 0);
}
};
等会儿研究一下动态规划;
当用到备忘缓存记忆递归的时候,和动态规划能够联想到一起了,其实递归中的备忘缓存不就是记录状态的数组吗?
考虑动态规划,就得考虑初始化和状态转移
状态转移:
在递归的时候已经明了:
*1: (s[i - 1] == p[j - 1] || p[j - 1] == '?') 则dp[i][j] = dp[i - 1][j - 1];
*2: (p[j - 1] == '*') 则dp[i][j] = dp[i][j-1] || dp[i-1][j];
*否则说明匹配失败
初始化:
因为是用dp[ls+1][lp+1]记录状态,所以必须自己先初始化第0行以及第0列
第0列表示s不为空,p为空,肯定为0
第0行表示s为空,p不为空,则p为*, **, ***...时为1,否则为0
dp[0][0]表示s和p都为空,为1
代码:
class Solution {
public:
bool isMatch(string s, string p) {
int ls = s.size(), lp = p.size();
if((s == p) || (p == "*")) return 1;
if((ls == 0) || (lp == 0)) return 0;
int dp[ls+1][lp+1];
memset(dp, 0, sizeof(dp));
dp[0][0] = 1;
//初始化第0行dp[0][j],像*,**,***...都为1;
//第0列dp[i][0]为0,数组初始化的时候已经初始化;
for (int j = 1; j <= lp; j++) {
if (dp[0][j - 1] && p[j - 1] == '*') {
dp[0][j] = 1;
}
}
for (int i = 1; i <= ls; ++ i) {
for (int j = 1; j <= lp; ++ j) {
if (s[i - 1] == p[j - 1] || p[j - 1] == '?') {
dp[i][j] = dp[i - 1][j - 1];
}else if (p[j - 1] == '*') {
dp[i][j] = dp[i][j-1] || dp[i-1][j];
}
}
}
return dp[ls][lp];
}
};
跳跃游戏 II

看到这道题,感觉和之前力扣杯的最小跳跃次数差不多,加上昨天被恶心的通配符匹配问题,所以想都没想,动态规划,初始化,状态转移一气呵成,示例ac,提交,超时!!!! 心态崩溃
最后选择正向的贪心算法解决这道题,也就是记录当前这步能够到达的最远距离,然后在遍历到达这步最远距离的时候,记录下一步能够到达的距离,当能够到达的最远距离大于等于数组的最后一位时,循环结束
AC代码:
class Solution {
public:
int jump(vector<int>& nums) {
// 被超时抛弃的动态规划,流下了不学无术的眼泪
// int n = nums.size() - 1;
// int dp[n+1];
// memset(dp, n, sizeof(dp));
// dp[n] = 0;
// for(int j = n - 1; j != -1; --j) {
// if(nums[j] + j >= n) dp[j] = 1;
// else dp[j] = dp[nums[j]+j] + 1;
// if(nums[j] > 1) {
// for(int i = j + 1; i <= n && i <= j+nums[j]; ++i) {
// if(dp[i] > dp[j]) dp[i] = dp[j];
// }
// }
// }
// return dp[0];
int maxPos = 0, n = nums.size(), end = 0, step = 0, i = 0;
while (end < n - 1) {
//寻找以i为下标的 i 到 i+nums[i] 之间能够达到的最远距离
maxPos = max(maxPos, i + nums[i]);
//第step + 1次跳跃结束
if (i == end) {
end = maxPos;
++step;
}
++i;
}
return step;
}
};
全排列

解题思路,最基础的全排列问题,递归排列出所有可能性,有重复的数字则不考虑;
AC代码:
class Solution {
public:
vector<vector<int>> res;
vector<int> ope;
void recursive(vector<int>& nums) {
if(ope.size() == nums.size()) {
res.push_back(ope);
return;
}
for(int i = 0; i < nums.size(); ++i) {
if(find(ope.begin(), ope.end(), nums[i]) != ope.end()) continue;
ope.push_back(nums[i]);
recursive(nums);
ope.pop_back();
}
}
vector<vector<int>> permute(vector<int>& nums) {
recursive(nums);
return res;
}
};
全排列 II

和上一道题不一样的地方就是,序列包含可重复数字。所以必定会存在剪枝的操作,最容易想到的就是在存结果的时候,判断序列是否存在,存在则不再存,但是这样做肯定也是超时的。所以这道题的关键在于如何剪枝,参考上一题的题解,动态的维护数组来获得全排列,可以利用set来标记当前位置数字是否重复出现。
利用set记录每一层迭代,也就是每个位置在迭代的过程中不能出现重复的数字,就是序列中每个位置对于相同的数字,只允许放一次,不允许放第二次。
AC代码:
class Solution {
public:
vector<vector<int>> res;
vector<int> ope;
void back(vector<int>& nums, int first, int end) {
if(first == end) {
res.push_back(nums);
return;
}
set<int> si;
for(int i = first; i < end; ++i) {
if(si.find(nums[i]) != si.end()) continue;
else {
swap(nums[i], nums[first]);
back(nums, first+1, end);
swap(nums[i], nums[first]);
si.insert(nums[i]);
}
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
back(nums, 0, nums.size());
return res;
}
};
旋转图像

解题思路,因为看到题目要求加上看到实例后,思路就固定到了每一行都会变成每一列,所以不难想到转置,正常的思路就是,转置之后然后交换列。但是我在考虑的时候直接想一步到位,然后然后写到后面就是成了三不像,但是大概的过程如下
/*
1 2 3 9 6 3 7 4 1
4 5 6 -> 8 5 2 -> 8 5 2
7 8 9 7 4 1 9 6 3
*/
AC代码:
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
if(matrix.size() <= 1) return;
int n = matrix.size();
for(int i = 0; i < n - 1; ++i) {
for(int j = 0, k = n-1; j < n - i - 1; ++j, --k) {
swap(matrix[i][j], matrix[k][n-i-1]);
}
}
for(int i = 0; i < n; ++i) {
for(int j = 0, k = n - 1; j < k; ++j, --k) {
swap(matrix[j][i], matrix[k][i]);
}
}
}
};
总的来说,这道题难度不大,在于理解矩阵的操作即可。
看到题解后才理解旋转的真正意义,大概如下:
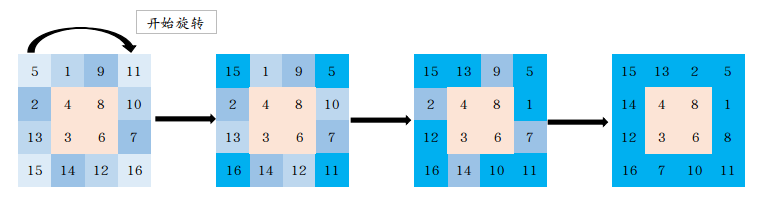
就是从外层开始旋转,直到旋转完毕,开始下一层,结束的条件是旋转的层只含有四个数,旋转结束后就可到答案
字母异位词分组

解题思路,既然是有一个标准来划分不同的组,想法肯定是先找到每个成员的相同点,然后根据相同点分组,最后合并成一个组。所以,三步走:
- 找到相同点,每个成员按字典序排列后相同;
- 根据成员的字典序划分小组
- 将多个小组合并成一个小组
需要注意的点:允许相同的成员,所以第一步需要声明成multimap
AC代码如下:
class Solution {
public:
vector<vector<string>> groupAnagrams(vector<string>& strs) {
multimap<string, string> h;
map<string, vector<string> > restmp;
vector<vector<string>> res;
//找到每个成员的字典序
for(auto first = strs.begin(); first != strs.end(); ++first) {
string tmp = *first;
sort(tmp.begin(), tmp.end());
h.insert(make_pair(*first, tmp));
}
//按字典序划分小组
for(auto scan = h.begin(); scan != h.end(); ++scan) {
restmp[scan->second].push_back(scan->first);
}
//合并成一个组得到答案
for(auto scan = restmp.begin(); scan != restmp.end(); ++scan) {
res.push_back(scan->second);
}
return res;
}
};
Pow(x, n)

解题思路,一开始想的就是递减n一直做乘法。不出意外的超时了。结合二分法的思想,可以一半一半的乘上去,这样可以节约一段时间。
ps,在处理int类型越界的情况,如果不借助转换,最好都利用负数进行操作。
AC代码:
class Solution {
public:
double resGet(double x, int n) {
if(n == 0) return 1;
double y = resGet(x, n/2);
return n % 2 == 0 ? y * y : y * y * x;
}
double myPow(double x, int n) {
if(x == 0) return 0;
if(x == 1 || x == -1) {
if(n % 2 == 1) return x;
else return 1;
}
int sign = -1;
if(n > 0) {
n = -1 * n;
sign = 1;
}
double res = resGet(x, n);
if(sign == 1)
return res;
else {
return 1/res;
}
}
};
另一种解题方案:
求x^N^次方,可以把x^N^拆分成多个x^y^相乘。
而在计算的时候,比较容易的的就是求出x^2^,x^4^,,x^8^ …
所以可以想办法把N分成2的幂次方相加,而这其实也就是把N转成二进制;
例如77,二进制为1001101,所以77 = 2 + 4 + 8 +64;
那么x^77^=x^2^x^4^x^8^*x^64^
这样就可以在求2的幂次方的x的时候,选择正确的结果进行相乘得到结果。
妙!





