@TOC
旋转链表

解题思路,看到旋转链表,想到的解法就是把这个链表当成一个环形链表,然后根据k找到这个环形链表的开始节点即可得到解。
AC代码:
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode* rotateRight(ListNode* head, int k) {
int length = 0;
ListNode* tmp = head;
ListNode* res = head;
ListNode* end;
while(tmp != NULL) {
++length;
end = tmp;
tmp = tmp->next;
}
//链表长度小于2或者k==0 直接返回
if(length < 2 || k == 0) return head;
//形成一个环形链表
end->next = head;
//找到向右移动k个位置后开始的节点
int start = k % length;
for(int i = 0; i < length - start; ++ i) {
tmp = res;
res = res->next;
}
//打破环形链表
tmp->next = NULL;
return res;
}
};
不同路径

解题思路,用动态规划的思想,每个点的路径总数=该点左方的路径总数+该点上分的路径总数,即Map[i][j] = Map[i-1][j] + Map[i][j-1]。结合广度搜索的想法,顺便可以还求出到达每个点需要走的步数,不过感觉优点多余了。直接两个for循环动态规划貌似就能解决的问题,我把它弄复杂了。
AC代码:
class Solution {
public:
struct Point{
Point(int a, int b): x(a), y(b) { }
int x;
int y;
bool operator==(const Point& p) {
return this->x == p.x && this->y == p.y;
}
};
int uniquePaths(int m, int n) {
int Map[m][n];
memset(Map, 0, sizeof(Map));
vector<Point> q;
//default
Map[0][0] = 1;
Point p(0, 0);
q.push_back(p);
while(!q.empty()) {
int num = q.size();
for(int i = 0; i < num; ++i) {
int x = q.front().x;
int y = q.front().y;
q.erase(q.begin());
//to right
if(x + 1 < m) {
int l = 0, t = 0;
if(x >= 0) l = Map[x][y];
if(y-1 >= 0) t = Map[x+1][y-1];
Map[x+1][y] = l + t;
Point tmp(x+1, y);
if(find(q.begin(), q.end(), tmp) == q.end()) q.push_back(tmp);
}
//to buttom
if(y + 1 < n) {
int l = 0, t = 0;
if(x-1 >= 0) l = Map[x-1][y+1];
if(y >= 0) t = Map[x][y];
Map[x][y+1] = l + t;
Point tmp(x, y+1);
if(find(q.begin(), q.end(), tmp) == q.end()) q.push_back(tmp);
}
}
}
return Map[m-1][n-1];
}
};
简介版本
class Solution {
public:
int uniquePaths(int m, int n) {
int Map[m][n];
memset(Map, 0, sizeof(Map));
for(int i = 0; i < m; ++i) {
for(int j = 0; j < n; ++j) {
if(i == 0 || j == 0) Map[i][j] = 1;
else {
Map[i][j] = Map[i-1][j] + Map[i][j-1];
}
}
}
return Map[m-1][n-1];
}
};
不同路径 II

解题思路,和上一道题一样,利用动态规划,不过这道题会比上面的题多了一个判断条件。但是动态规划的思想不变,即每个点的路径总数=该点左方的路径总数+该点上分的路径总数,即Map[i][j] = Map[i-1][j] + Map[i][j-1]。
AC代码
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = (*obstacleGrid.begin()).size();
int Map[m][n];
memset(Map, 0, sizeof(Map));
for (int i = 0; i < m; ++i) {
for(int j = 0; j < n; ++j) {
if(obstacleGrid[i][j] == 1) {
Map[i][j] = 0;
continue;
}
if(i == 0 && j == 0) Map[i][j] = 1;
else if(i == 0) Map[i][j] = Map[i][j-1];
else if(j == 0) Map[i][j] = Map[i-1][j];
else Map[i][j] = Map[i-1][j] + Map[i][j-1];
}
}
return Map[m-1][n-1];
}
};
最小路径和

解题思路,一样的思想,一样的套路,只不过把路径的总数改成路径的权数。
AC代码:
class Solution {
public:
int minPathSum(vector<vector<int>>& grid) {
int m = grid.size();
int n = (*grid.begin()).size();
int Map[m][n];
memset(Map, 0, sizeof(Map));
for(int i = 0; i < m; ++i) {
for(int j = 0; j < n; ++j) {
if(i == 0 && j == 0) Map[i][j] = grid[i][j];
else if(i == 0) Map[i][j] = grid[i][j] + Map[i][j-1];
else if(j == 0) Map[i][j] = grid[i][j] + Map[i-1][j];
else Map[i][j] = grid[i][j] + min(Map[i-1][j], Map[i][j-1]);
}
}
return Map[m-1][n-1];
}
};
有效数字

之前解题的时候遇到过根据自动机解题的,所以这道题的思路就是利用自动机,但是在写自动机的时候,脑袋都大了,状态有点小多,最后还是找到评论里的一个状态机完成的。

AC代码:
class Solution {
public:
bool isNumber(string s) {
vector<map<string, int>> FSM;
FSM.push_back({make_pair("blank", 0), make_pair("dot", 3), make_pair("sign", 1), make_pair("num", 2)});
FSM.push_back({make_pair("num", 2), make_pair("dot", 3)});
FSM.push_back({make_pair("blank", 8), make_pair("dot", 4), make_pair("e", 5), make_pair("num", 2)});
FSM.push_back({make_pair("num", 4)});
FSM.push_back({make_pair("blank", 8), make_pair("e", 5), make_pair("num", 4)});
FSM.push_back({make_pair("sign", 6), make_pair("num", 7)});
FSM.push_back({make_pair("num", 7)});
FSM.push_back({make_pair("num", 7), make_pair("blank", 8)});
FSM.push_back({make_pair("blank", 8)});
int curstatus = 0;
string nextstatus;
for(int i = 0; i < s.size(); ++i) {
if(s[i] == ' ') nextstatus = "blank";
else if(s[i] == '+' || s[i] == '-') nextstatus = "sign";
else if(s[i] == 'e') nextstatus = "e";
else if(s[i] == '.') nextstatus = "dot";
else if(s[i] >= '0' && s[i] <= '9')nextstatus = "num";
else return false;
if(FSM[curstatus].find(nextstatus) == FSM[curstatus].end()) return false;
else curstatus = FSM[curstatus][nextstatus];
}
if(curstatus == 2 || curstatus == 4 || curstatus == 7 || curstatus == 8) return true;
return false;
}
};
加一

这道题应该算是弟中弟级别了,只需要考虑进位就ok了
AC代码
class Solution {
public:
vector<int> plusOne(vector<int>& digits) {
for(int i = digits.size() - 1; i >= 0; --i) {
int tmp = digits[i] + 1;
if(tmp != 10) {
digits[i] = tmp;
return digits;
}else {
digits[i] = 0;
}
}
digits.insert(digits.begin(), 1);
return digits;
}
};
二进制求和

这道题需要注意的也就只有进位了,思考难度不算大,直接模拟加法就可以了。
AC代码
class Solution {
public:
string addBinary(string a, string b) {
if(a.size() > b.size()) {
string tmp = a;
a = b;
b = tmp;
}
int lmin = a.size();
int lmax = b.size();
a.insert(a.begin(), lmax - lmin, '0');
int carry = 0;
for(int i = lmax - 1; i >= 0; --i) {
a[i] = a[i] + b[i] + carry - '0';
if(a[i] >= '2') {
a[i] = (a[i]=='2' ? '0' : '1');
carry = 1;
}else {
carry = 0;
}
}
if(carry == 1) a.insert(a.begin(), '1');
return a;
}
};
文本左右对齐

解题思路就是,记录两个值,一是单词的个数,而是这些单词的长度。然后根据最大长度以及单词个数和总长度判断单词之间需要填充的空格数。
填充的空格数可以利用求余和求商解决。这里需要根据单词个数判断。
AC代码:
class Solution {
public:
vector<string> fullJustify(vector<string>& words, int maxWidth) {
vector<string> res;
//记录每一行的单词,以及单词的个数
vector<string> line;
//用于判断是否还能往这行中存单词
int len = 0;
//记录单词总长度
int wordsize = 0;
for(auto iter = words.begin(); iter != words.end(); ++iter) {
if(len + (*iter).size() <= maxWidth) {
line.push_back(*iter);
len = len + (*iter).size() + 1;
wordsize += (*iter).size();
}else {
int blank = maxWidth - wordsize;
int num = line.size();
string tmp;
if(num == 1) {
tmp = line[0].append(maxWidth-line[0].size(), ' ');
}else {
int bn = blank / (num-1);
int bm = blank % (num-1);
for(auto s : line) {
tmp += s;
tmp.append(bn, ' ');
if(bm != 0) {
tmp.append(1, ' ');
--bm;
}
}
tmp = tmp.substr(0, maxWidth);
}
res.push_back(tmp);
line.erase(line.begin(), line.end());
line.push_back(*iter);
wordsize = (*iter).size(), len = wordsize + 1;
}
}
//处理最后一行
if(line.size() != 0) {
string last;
for(auto s : line) last = last + s + ' ';
if(last.size() < maxWidth)
last = last.append(maxWidth-last.size(), ' ');
else
last = last.substr(0, maxWidth);
res.push_back(last);
}
return res;
}
};
x 的平方根

看到这道题,想到的就是二分法,但是在用的时候需要注意两个地方,一是考虑0和1特殊情况,二是考虑整数类型溢出的情况,把这两个情况考虑进去则就没问题了
AC代码:
class Solution {
public:
int mySqrt(int x) {
if (x < 2) return x==1?1:0;
int left = 0, right = x;
while(left < right) {
int mid = left + (right - left) / 2;
if((long long)mid * mid <= x) {
left = mid + 1;
} else {
right = mid;
}
}
return left - 1;
}
};
爬楼梯
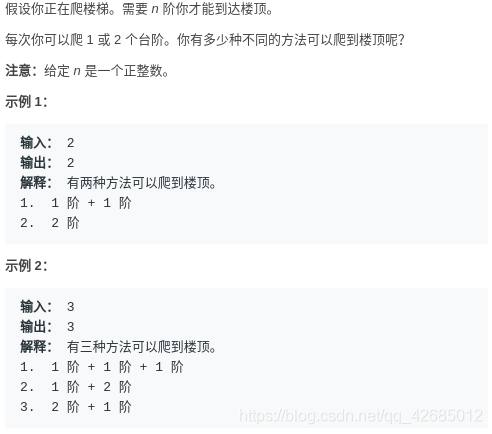
解题思路,利用动态规划的思想,因为可以爬 1 或 2 个台阶,所以每个台阶的步数等于上面一个台阶的步数+上面两个台阶的步数。
AC代码:
class Solution {
public:
int climbStairs(int n) {
int db[n+2];
memset(db, 0, sizeof(db));
db[n] = 1;
for(int i = n-1; i >= 0; --i) {
db[i] = db[i+1] + db[i+2];
}
return db[0];
}
};





